Publications
Research contributions in AI4Science and ML optimization
Each publication includes research diagrams and video explanations of key concepts (videos being added progressively)
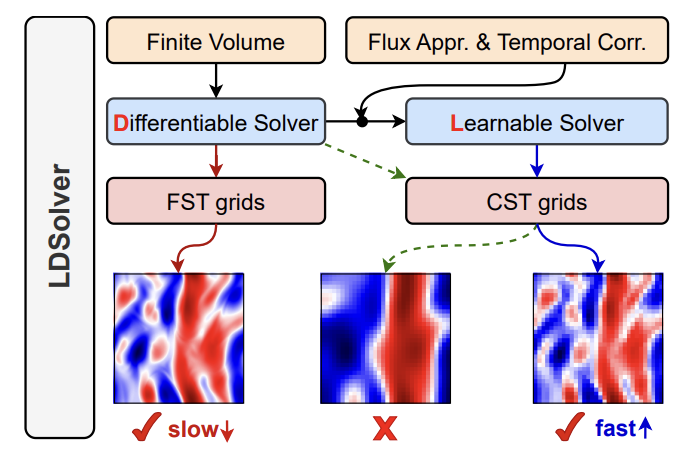
Learnable-Differentiable Finite Volume Solver for Accelerated Simulation of Flows
Authors: Mengtao Yan, Qi Wang, Haining Wang, Ruizhi Chengze, Yi Zhang, Hongsheng Liu, Zidong Wang, Fan Yu, Qi Qi, Hao Sun
Proceedings of the 31st ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD) 2025
We present a novel learnable-differentiable finite volume solver that significantly accelerates computational fluid dynamics simulations. By combining traditional finite volume methods with differentiable programming and machine learning techniques, our approach enables end-to-end optimization of flow simulations while maintaining physical accuracy and computational efficiency.
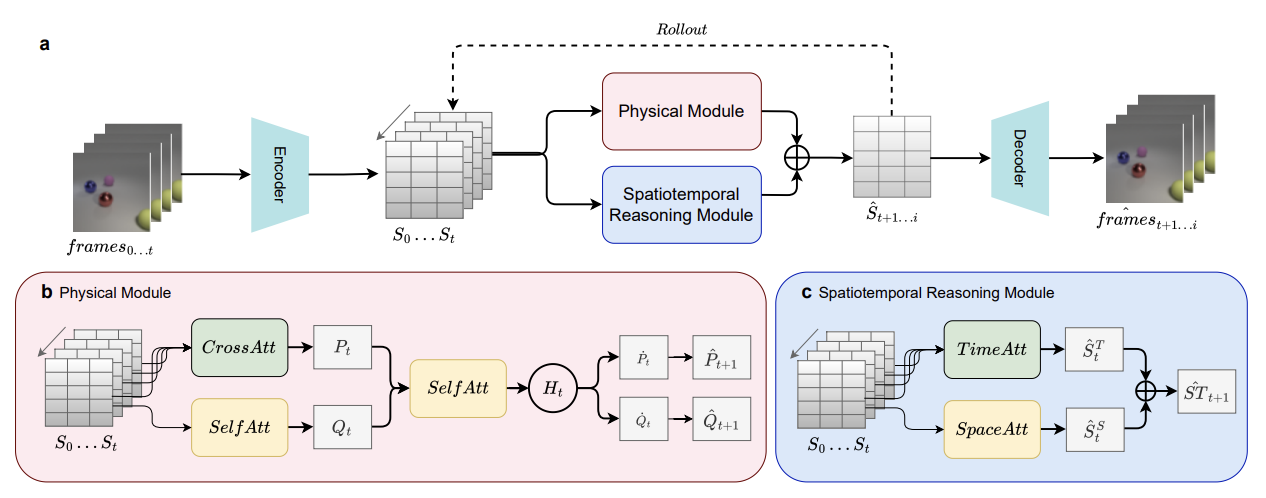
SlotPi: Physics-informed Object-centric Reasoning Models
Authors: Jian Li, Wan Han, Ning Lin, Yu-Liang Zhan, Ruizhi Chengze, Haining Wang, Yi Zhang, Hongsheng Liu, Zidong Wang, Fan Yu, Hao Sun
Proceedings of the 31st ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD) 2025
We introduce SlotPi, a novel physics-informed framework that combines object-centric representation learning with physical reasoning. By integrating physics principles into slot attention mechanisms, our approach enables more interpretable and physically consistent object-centric reasoning in complex dynamic systems.
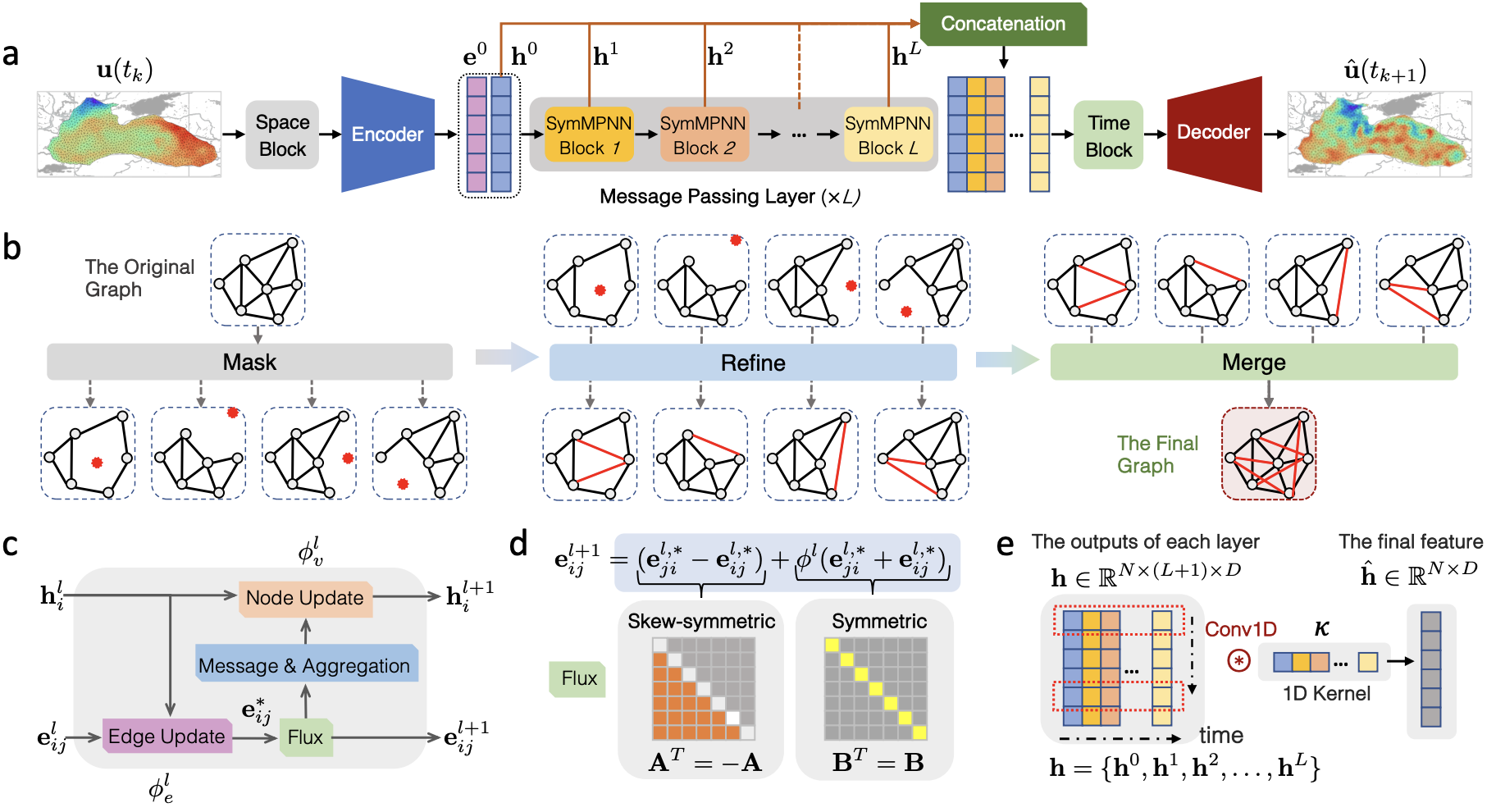
Conservation-informed Graph Learning for Spatiotemporal Dynamics Prediction
Authors: Yuan Mi, Pu Ren, Hongteng Xu, Hongsheng Liu, Zidong Wang, Yike Guo, Ji-Rong Wen, Hao Sun, Yang Liu
Proceedings of the 31st ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD) 2025
We present a novel conservation-informed graph learning approach for predicting spatiotemporal dynamics in complex systems. By incorporating physical conservation laws into graph neural networks, our method achieves superior accuracy in modeling spatiotemporal phenomena while maintaining physical consistency, advancing the field of AI4Science.
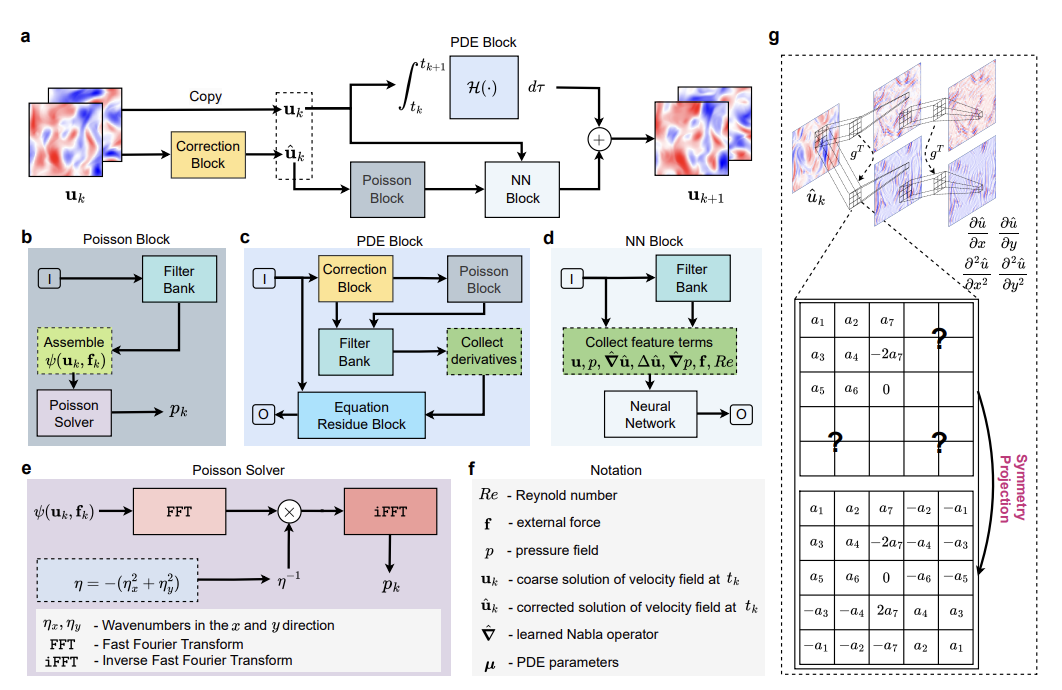
P²C Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics
Authors: Qi Wang, Pu Ren, Haoyu Zhou, Xiao-Yu Liu, Zidong Deng, Yi Zhang, Ruizhi Chengze, Hongsheng Liu, et al.
Advances in Neural Information Processing Systems (NeurIPS) 2024
We introduce P²C Net, a novel PDE-preserved coarse correction network that efficiently predicts spatiotemporal dynamics. Our method combines coarse-scale predictions with fine-scale corrections while preserving the underlying physical constraints, achieving significant computational speedup without sacrificing accuracy in spatiotemporal modeling tasks.
PhyMPGN: Physics-encoded Message Passing Graph Network for spatiotemporal PDE systems
Authors: Bindi Zeng, Qi Wang, Mengtao Yan, Yang Liu, Ruizhi Chengze, Yi Zhang, Hongsheng Liu, Zidong Wang, et al.
International Conference on Learning Representations (ICLR) 2025
We present PhyMPGN, a physics-encoded message passing graph network designed for solving spatiotemporal PDE systems. Our approach integrates physical principles directly into the message passing framework, enabling more accurate and physically consistent predictions for complex spatiotemporal dynamics while maintaining computational efficiency.
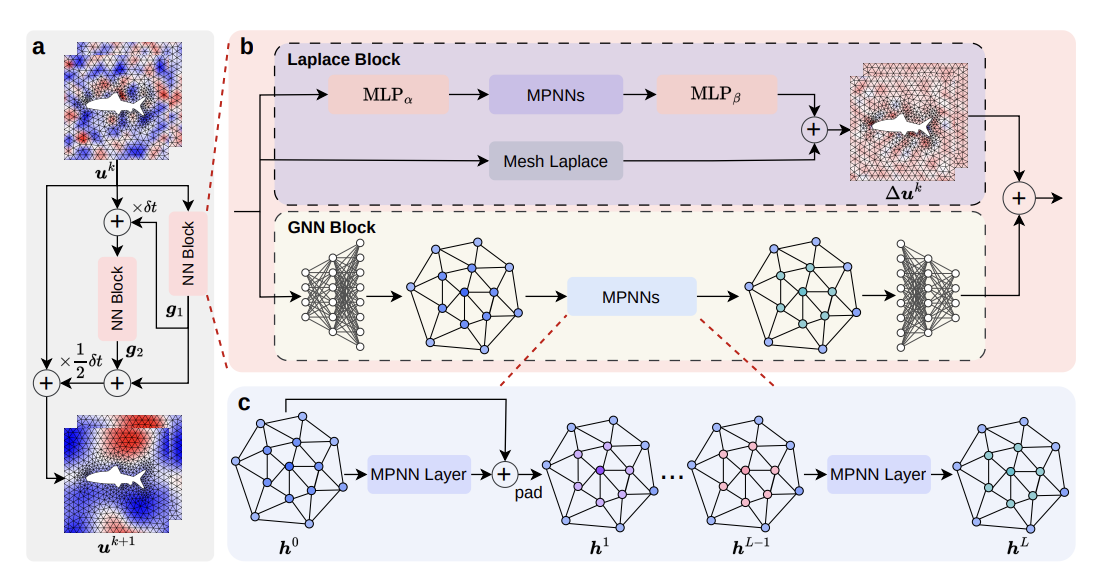
PDEformer: Towards a Foundation Model for One-Dimensional Partial Differential Equations
Authors: Zhanhong Ye, Xiang Huang, Lei Chen, Hongsheng Liu, Zidong Wang, Bin Dong
International Conference on Learning Representations (ICLR) 2024 Workshops
We present PDEformer, a transformer-based foundation model designed specifically for solving one-dimensional partial differential equations. By leveraging the transformer architecture's sequence modeling capabilities, our approach demonstrates strong generalization across diverse PDE families and boundary conditions, paving the way for unified neural PDE solvers.
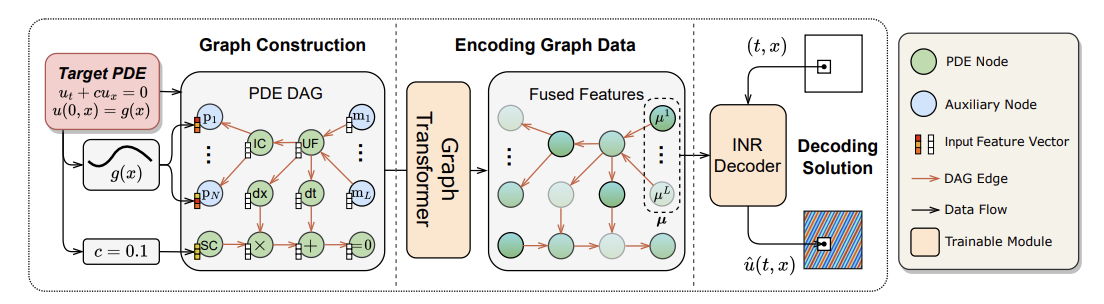
Prediction of transonic flow over supercritical airfoils using geometric-encoding and deep-learning strategies
Authors: Zhiwen Deng, Jing Wang, Hongsheng Liu, Hairun Xie, BoKai Li, Miao Zhang, Tingmeng Jia, Yi Zhang, Zidong Wang, Bin Dong
Physics of Fluids 35, 075146 (2023)
We present a novel approach for predicting transonic flow over supercritical airfoils using geometric-encoding and deep-learning strategies. Our method combines advanced geometric encoding techniques with deep neural networks to accurately predict complex flow patterns around airfoils, enabling efficient aerodynamic analysis and design optimization for transonic flight conditions.
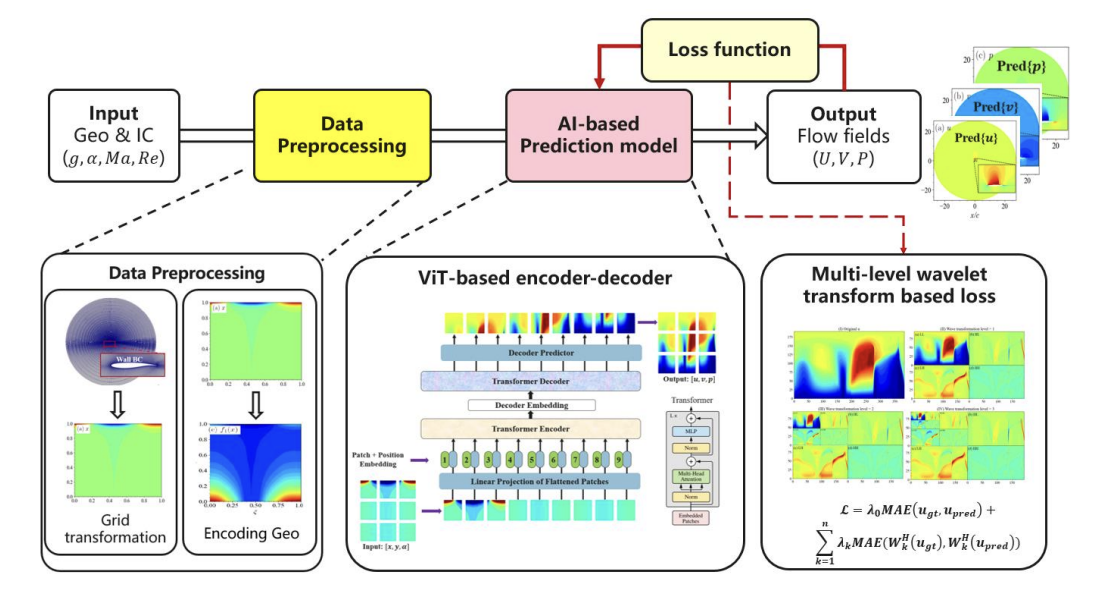
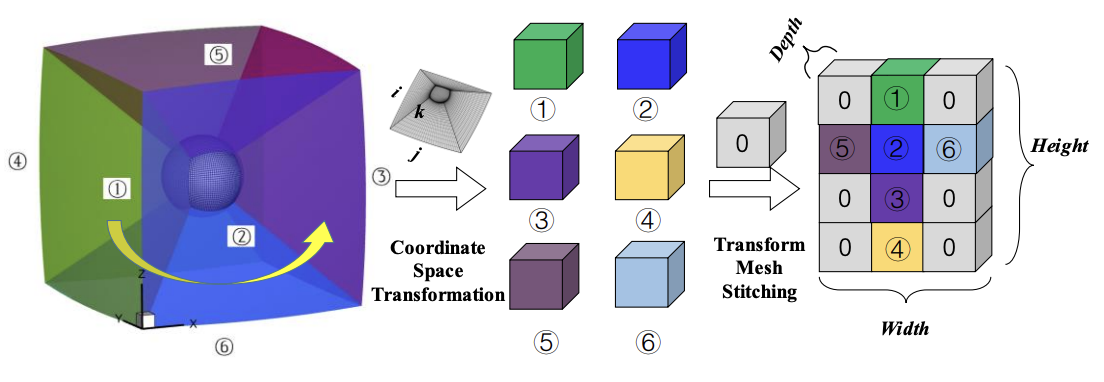
Deep learning-based reduced order model for three-dimensional unsteady flow using mesh transformation and stitching
Authors: Xin Li, Zhiwen Deng, Rui Feng, Ziyang Liu, Renkun Han, Hongsheng Liu, Gang Chen
Computers & Fluids 2024
We present a novel deep learning-based reduced order model for three-dimensional unsteady flow simulation. Our approach combines mesh transformation techniques with stitching methods to efficiently model complex fluid dynamics, enabling fast and accurate predictions of unsteady flows while maintaining computational efficiency and physical accuracy.
Transportation origin-destination demand estimation with quasi-sparsity
Authors: Jingxing Wang, Shu Lu, Hongsheng Liu, Xuegang Ban
Transportation Science 57 (2), 289-312 (2023)
We propose a novel approach for transportation origin-destination (OD) demand estimation using quasi-sparsity techniques. Our method addresses the challenge of estimating OD flows in transportation networks by leveraging advanced optimization algorithms and sparsity constraints, enabling more accurate and efficient transportation planning and traffic management.
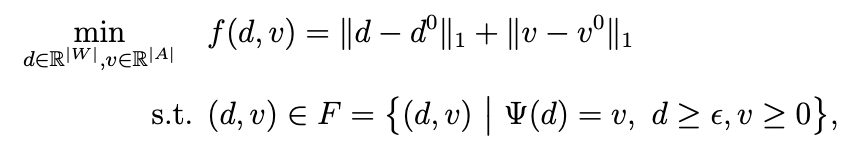
Meta-auto-decoder for solving parametric partial differential equations
Authors: Xiang Huang, Zhanhong Ye, Hongsheng Liu, Shi Ji, Zidong Wang, Kang Yang, Yang Li, Min Wang, Haotian Chu, Fan Yu, Bei Hua, Lei Chen, Bin Dong
Advances in Neural Information Processing Systems (NeurIPS) 2022
We introduce Meta-auto-decoder, a novel meta-learning framework for solving parametric partial differential equations (PDEs). Our approach combines meta-learning with auto-decoder architectures to efficiently adapt to new PDE parameters and boundary conditions, enabling rapid solution of parametric PDE families with minimal computational overhead and superior generalization capabilities.

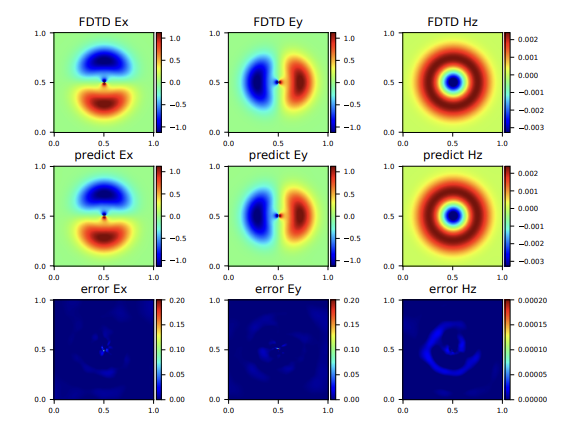
A Universal PINNs Method for Solving Partial Differential Equations with a Point Source
Authors: Xiang Huang, Hongsheng Liu, Boming Shi, Zidong Wang, Kang Yang, Yang Li, Min Wang, Haotian Chu, Jing Zhou, et al.
Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence (IJCAI-22)
We propose a universal Physics-Informed Neural Networks (PINNs) method for solving partial differential equations with point sources. Our approach addresses the challenge of handling singular point sources in PDEs by developing a novel neural network architecture that can effectively capture the complex behavior around singularities while maintaining high accuracy across the entire domain.
Convergence of the augmented decomposition algorithm
Authors: Hongsheng Liu, Shiqian Lu
Computational Optimization and Applications 72 (1), 179-213 (2019)
We analyze the convergence properties of the augmented decomposition algorithm for solving large-scale optimization problems. Our theoretical analysis provides convergence guarantees and establishes convergence rates for this important class of decomposition methods, with applications to distributed optimization and ML infrastructure.
